Problem Description

You are given a triangle tower of $n$ layers. There are $i$ vertices in the $i$-th layer, and at each vertex there is an integer written on it.

Below is a figure for $n=4$.


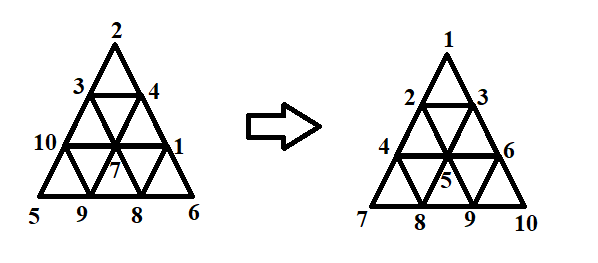
It can be shown that there are a total of $\dfrac{n(n+1)}{2}$ vertices. We guarantee that the numbers are a permutation of all integers in $[1,\dfrac{n(n+1)}{2}]$.

You need to sort the numbers, first by row and second by column, with some numbers of **triangle rotations**. A triangle rotation means:

- Select a unit triangle (the smallest non-zero triangle you can find in the figure) and rotate the numbers on its three vertices **clockwise**.

Determine whether there exists a way to sort the numbers within $2n^3$ operations. If yes, print out one of them.

Input

The first line contains an integer $T(1\leq T \leq 150)$ - the number of test cases.

The first line of each test case contains an integer $n(2\leq n \leq 50)$ - the number of layers of the tower.

The next $n$ lines of each test case represent the numbers in the tower. The $i$-th line contains $i$ numbers.

It is guaranteed that $\sum n^3 \leq 10^6$.

Output

For each test case, Output "Yes" or "No" in a single line, indicating whether there exists a way to sort the numbers within $2n^3$ operations.

If your answer is "Yes", Output an integer $k(0\leq k \leq 2n^3)$ - the number of operation you used in a single line.

For the next $k$ lines, output three integers $x,y(1 \leq x \leq n-1,1\leq y \leq 2x-1)$, indicating an operation at the $y$-th triangle between the $x$-th layer and the $x+1$-th layer.

3
3
6
4 5
2 1 3
2
2
1 3
2
2
3 1

Yes
11
2 3
1 1
1 1
2 3
2 3
2 2
2 1
2 1
2 2
2 3
2 3
No
Yes
2
1 1
1 1